Finite Field Arithmetic

This section describes the Intel® Integrated Performance Primitives Cryptography (Intel® IPP Cryptography) functions that implement arithmetic operations with elements of the following finite fields [ANT]:

GF(p)

A finite field of p elements.

GF(q)

If q is an odd prime number, then the finite field is represented by integers modulo q. This field is also known as the prime finite field.

GF(pd)

If p = q, q is an odd prime number and d > 1, the finite field is represented by polynomials modulo g(x), GF(p)[x]/g(x), where g(x) is an irreducible polynomial over GF(p). This field is also known as a degree ``d`` extension of the GF(``p``) field.

GF(((qn1)n2)n3)

A very complex extension of the prime finite field GF(q). The initial prime field GF(q) used at the lowest level of the construct is frequently called the basic finite field with respect to the extension.

The finite field arithmetic functions use context structures of the IppsGFpState and IppsGFpElement types to store data of the finite field and the field elements, respectively.

The IppsGFpElement type structure is used for internal representation of field elements. In application (or external) representation of field element is straightforward. Each element E of the prime field GF(q) is an unsigned number in the range [0, q - 1], which is represented by a data array Ipp32u qe[len32] , so that

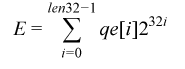
image1

where 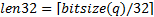image2 is the length of the prime q, expressed in dwords (32-bit chunks).

Each element E of GF(pd) is represented by a polynomial of degree less than d. This polynomial is represented by an array of coefficients pe[d] that belong to GF(p).

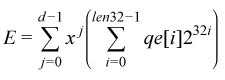
image3

Thus,

Ipp32u a[4] = {0xBFF9AEE1,0xBF59CC9B,0xD1B3BBFE,0xD6031998};

is an external (application-side) representation of an element that belongs to some prime field GF(q), bitsize(q)=128.

Similarly,

Ipp32u b[2][4] = { {0xBFF9AEE1,0xBF59CC9B,0xD1B3BBFE,0xD6031998},
                   {0xBB6D8A5D,0xDC2C6558,0x80D02919,0x5EEEFCA3} };

is an external (application-side) representation of an element that belongs to GF(q2) - a degree 2 extension of some prime field GF(q), bitsize(q)=128.

You can use Intel IPP Cryptography finite field functions to convert between the internal and the external representations of a finite field element.

Prime finite fields are the basic mathematical objects of Elliptic Curve (EC) cryptography. Intel IPP Cryptography supports different kinds of EC over finite fields and, in particular, the standard elliptic curves - elliptic curves with pre-defined parameters, including the underlying finite field. The performance of EC functionality directly depends on the efficiently of the implementation of operations with finite field elements such as addition, multiplication, and squaring.

Intel IPP Cryptography contains several different optimized implementations of finite field arithmetic functions. These implementations, referred to in this document as “methods”, are grouped together in structures. Intel IPP Cryptography does not reveal the content of these structures. The implementations, including those optimized for a particular prime q, are accessed by special Intel IPP Cryptography functions. For example, ippsGFpMethod_p192r1() returns a pointer to the structure containing optimized arithmetic over prime p192r1 (see GFpMethod for details).

Similarly, for GF(pd), additional knowledge concerning the predefined field polynomial g(x) allows Intel IPP Cryptography to provide a more efficient implementation of finite field arithmetic than in the case of an arbitrary field polynomial g(x). Intel IPP Cryptography contains methods dedicated to certain predefined g(x). For example, the functions ippsGFpxMethod_binom2() returns a pointer to the structure containing optimized arithmetic over GF(p2).

The comparison function GFpCmpElement returns the result of comparison:

#define IPP_IS_EQ (0) // elements are equal
#define IPP_IS_GT (1) // the first element is greater than the second one
#define IPP_IS_LT (2) // the first element is less than the second one
#define IPP_IS_NE (3) // elements are not equal
#define IPP_IS_NA (4) // elements are not comparable

Product and Performance Information

Performance varies by use, configuration and other factors. Learn more at www.intel.com/PerformanceIndex. Notice revision #20201201

previous

ECCGetResultString

next

GFpInit