How-Tos

How to Do Dynamic Indexing

This tutorial will show you how to create a dynamic index, add and remove vectors, search the index, save and reload it.

Generating test data

We generate a sample dataset using the svs.generate_test_dataset() generation function. This function generates a data file, a query file, and the ground truth. Note that this is randomly generated data, with no semantic meaning for the elements within it.

We first load svs and other modules required for this example.

import os
import svs
import numpy as np

Then proceed to generate the test dataset.

# Create a test dataset.
# This will create a directory "example_data_vamana" and populate it with three
# entries:
# - data.fvecs: The test dataset.
# - queries.fvecs: The test queries.
# - groundtruth.ivecs: The groundtruth.
test_data_dir = "./example_data_vamana"
svs.generate_test_dataset(
    10000,                      # Create 10000 vectors in the dataset.
    1000,                       # Generate 1000 query vectors.
    128,                        # Set the vector dimensionality to 128.
    test_data_dir,              # The directory where results will be generated.
    data_seed = 1234,           # Random number seed for reproducibility.
    query_seed = 5678,          # Random number seed for reproducibility.
    num_threads = 4,            # Number of threads to use.
    distance = svs.DistanceType.L2,   # The distance type to use.
)

Building the Dynamic Index

To construct the index we first need to define the hyper-parameters for the graph construction (see How to Choose Graph Building Hyper-parameters for details).

In Python

This is done by creating an instance of svs.VamanaBuildParameters.

parameters = svs.VamanaBuildParameters(
    graph_max_degree = 64,
    window_size = 128,
)

Now that we’ve established our hyper-parameters, it is time to construct the index. For this, we load the data and build the dynamic index with the first 9k vectors of the dataset.

In Python

n = 9000
data = svs.read_vecs(os.path.join(test_data_dir, "data.fvecs"))
idx = np.arange(data.shape[0]).astype('uint64')

index = svs.DynamicVamana.build(
    parameters,
    data[:n],
    idx[:n],
    svs.DistanceType.L2,
    num_threads = 4,
)

Updating the index

Once we’ve built the initial dynamic index, we can add and remove vectors.

In Python

# Add the following 1000 vectors to the index.
index.add(data[n:n+1000], idx[n:n+1000])

# Remove the first 100 vectors from the index.
index.delete(idx[:100])

Deletions are performed in a lazy fashion to avoid an excessive compute overhead. When a vector is deleted, it is added to a list of deleted elements but not immediately removed from the index. At search time, it is used during graph traversal but it is filtered out from the nearest neighbors result. Once a sufficient number of deletions is accumulated the consolidate() and compact() functions should be ran to effectively remove the vectors from the index.

In Python

# Consolidate the index.
index.consolidate().compact(1000)

Searching the Index

First, we load the queries and the computed ground truth for our example dataset.

In Python

# Load the queries and ground truth.
queries = svs.read_vecs(os.path.join(test_data_dir, "queries.fvecs"))
groundtruth = svs.read_vecs(os.path.join(test_data_dir, "groundtruth.ivecs"))

Then, run the search in the same fashion as for the static graph.

In Python

# Set the search window size of the index and perform queries.
index.search_window_size = 30
I, D = index.search(queries, 10)

# Compare with the groundtruth.
recall = svs.k_recall_at(groundtruth, I, 10, 10)
print(f"Recall = {recall}")
assert(recall == 0.8202)

Saving the Index

If you are satisfied with the performance of the generated index, you can save it to disk to avoid rebuilding it in the future.

In Python

# Finally, we can save the results.
index.save(
    os.path.join(test_data_dir, "example_config"),
    os.path.join(test_data_dir, "example_graph"),
    os.path.join(test_data_dir, "example_data"),
)

Note

The save index function currently uses three folders for saving. All three are needed to be able to reload the index.

  • One folder for the graph.

  • One folder for the data.

  • One folder for metadata.

This is subject to change in the future.

Reloading a Saved Index

To reload the index from file, use the corresponding constructor with the three folder names used to save the index. Performing queries is identical to before.

In Python

# We can reload an index from a previously saved set of files.
index = svs.DynamicVamana(
    os.path.join(test_data_dir, "example_config"),
    svs.GraphLoader(os.path.join(test_data_dir, "example_graph")),
    svs.VectorDataLoader(
        os.path.join(test_data_dir, "example_data"), svs.DataType.float32
    ),
    svs.DistanceType.L2,
    num_threads = 4,
)

Note that the second argument, the one corresponding to the file for the data, requires a svs.VectorDataLoader and the corresponding data type.


How to Choose Graph Building Hyper-parameters

The optimal values for the graph building hyper-parameters depend on the dataset and on the trade-off between performance and accuracy that is required. We suggest here commonly used values and provide some guidance on how to adjust them. See How does graph building work? for more details about graph building.

  • graph_max_degree: Maximum out-degree of the graph. A larger graph_max_degree implies more distance computations per hop, but potentially a shorter graph traversal path, so it can lead to higher search performance. High-dimensional datasets or datasets with a large number of points usually require a larger graph_max_degree to reach very high search accuracy. Keep in mind that the graph size in bytes is given by 4 times graph_max_degree (each neighbor id in the graph adjacency lists is represented with 4 bytes) times the number of points in the dataset, so a larger graph_max_degree will have a larger memory footprint. Commonly used values for graph_max_degree are 32, 64 or 128.

  • alpha: Threshold for the graph adjacency lists pruning rule during the second pass over the dataset. For distance types favoring minimization, set this to a number greater than 1.0 to build a denser graph (typically, 1.2 is sufficient). For distance types preferring maximization, set to a value less than 1.0 to build a denser graph (such as 0.95).

  • window_size: Sets the search_window_size for the graph search conducted to add new points to the graph. This parameter controls the quality of graph construction. A larger window size will yield a higher-quality index at the cost of longer construction time. Should be larger than graph_max_degree.

  • max_candidate_pool_size: Limit on the number of candidates to consider for the graph adjacency lists pruning rule. Should be larger than window_size.

  • num_threads: The number of threads to use for index construction. The indexing process is highly parallelizable, so using as many num_threads as possible is usually better.

How to Set the Search Window Size

The search_window_size is the knob controlling the trade-off between performance and accuracy for the graph search. A larger search_window_size implies exploring more vectors, improving the accuracy at the cost of a longer search path. See How does the graph search work? for more details about graph search. One simple way to set the search_window_size is to run searches with multiple values of the parameter and print the recall to identify the required search_window_size for the chosen accuracy level.

In Python

# We can vary the search window size to demonstrate the trade off in accuracy.
for window_size in range(10, 50, 10):
    index.search_window_size = window_size
    I, D = index.search(queries, 10)
    recall = svs.k_recall_at(groundtruth, I, 10, 10)
    print(f"Window size = {window_size}, Recall = {recall}")

In C++

auto expected_recall =
    std::map<size_t, double>({{10, 0.5509}, {20, 0.7281}, {30, 0.8215}, {40, 0.8788}});
for (auto windowsize : {10, 20, 30, 40}) {
    recall = run_recall(index, queries, groundtruth, windowsize, 10, "Sweep");
    check(expected_recall.at(windowsize), recall);
}

How to Choose Compression Parameters

Number of bits per level

LVQ compression [ABHT23] comes in two flavors: one or two levels. One level LVQ, or LVQ-B, uses B bits to encode each vector component using a scalar quantization with per-vector scaling factors. Two level LVQ, or LVQ-B1xB2, uses LVQ-B1 to encode the vectors and a modification of LVQ to encode the residuals using B2 bits.

Whether using one or two levels, and the number of bits, depends on the dataset and the trade-off between performance and accuracy that needs to be achieved.

When using two-level LVQ, the graph search is conducted using vectors compressed with LVQ-B1 and a final re-ranking step is performed using the residuals compressed with B2 bits to improve the search recall. This decoupled strategy is particularly beneficial for high dimensional datasets (>200 dimensions) as LVQ achieves up to ~8x bandwidth reduction (B1=4) compared to a float32-valued vector. The number of bits for the residuals (4 or 8) should be chosen depending on the desired search accuracy. Suggested configurations for high dimensional vectors are LVQ-4x8 or LVQ-4x4 depending on the desired accuracy.

For lower dimensional datasets (<200 dimensions), one-level LVQ-8 is often a good choice. If higher recall is required, and a slightly larger memory footprint is allowed, then LVQ-8x4 or LVQ-8x8 should be used.

These are general guidelines, but the best option will depend on the dataset. If willing to optimize the search for a particular dataset and use case, we suggest trying different LVQ options. See SVS + Vector compression (large scale datasets) and SVS + Vector compression (small scale datasets) for benchmarking results of the different LVQ settings in standard datasets.

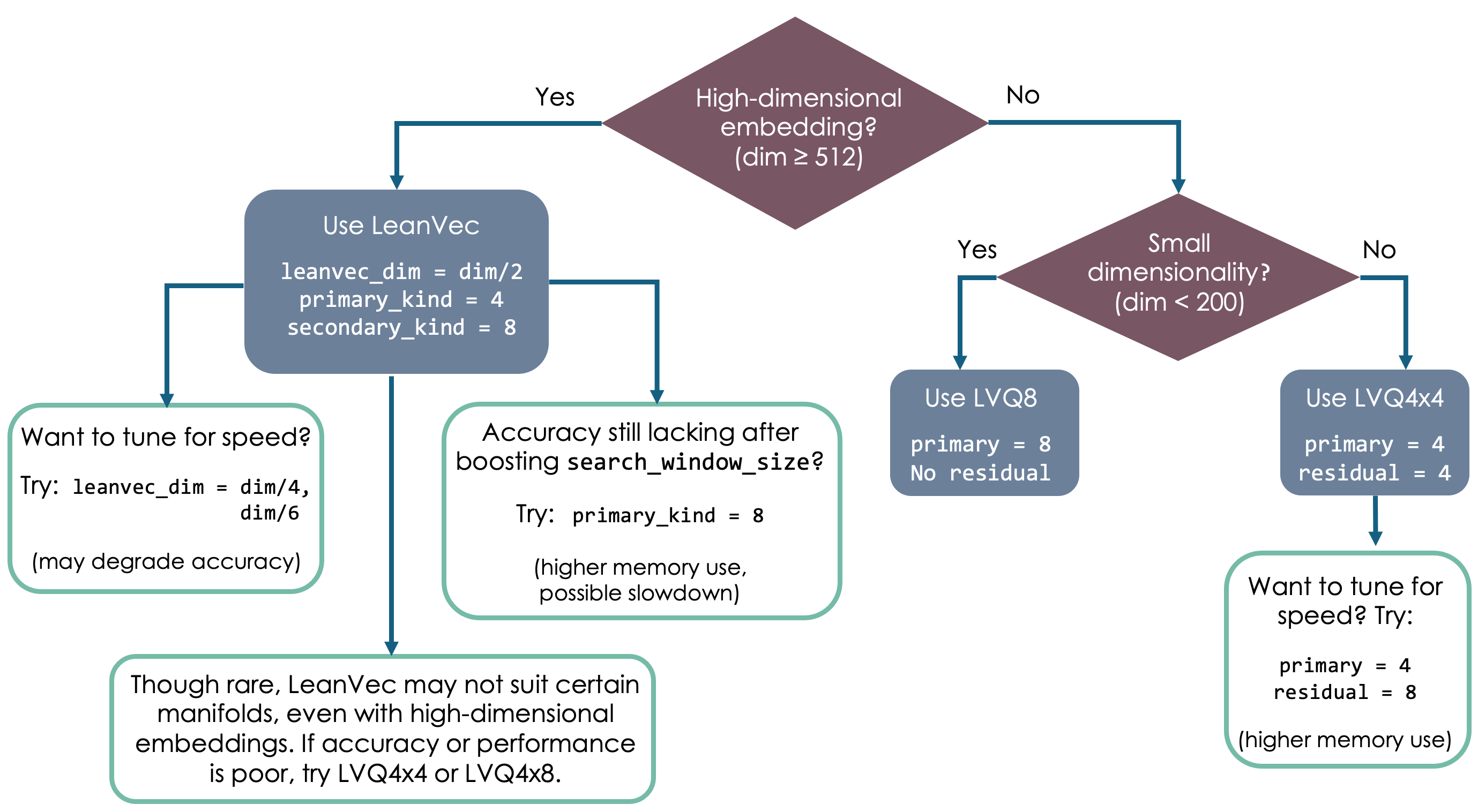
LVQ implementation strategy

The strategy argument in the svs.LVQLoader is of type svs.LVQStrategy and defines the low level implementation strategy for LVQ, whether it is Turbo or Sequential. Turbo is an optimized implementation that brings further performance over the default (Sequential) implementation [AHBW24]. Turbo can be used when using 4 bits for the primary LVQ level and it is enabled by default for that setting.

Padding

LVQ-compressed vectors can be padded to a multiple of 32 or 64 bytes to be aligned with half or full cache lines. This improves search performance and has a low impact on the overall memory footprint cost (e.g., 5% and 12% larger footprint for Deep with graph_max_degree = 128 and 32, respectively). A value of 0 (default) implies no special alignment.

For details on the C++ implementation see Locally-Adaptive Vector Quantization.

How to Prepare Your Own Vector Dataset

Preparing your own vector dataset is simple with our Python API svs, which can directly use embeddings encoded as numpy arrays.

There are 3 main steps to preparing your own vector dataset, starting from the original data format (e.g. images, text).

  1. Select embedding model

  2. Preprocess the data

  3. Embed the data to generate vectors

  4. Use or save the embeddings

We will walk through a simple example below. For complete examples, please see our VectorSearchDatasets repository, which contains code to generate compatible vector embeddings for common datasets such as open-images.

Example: vector embeddings of images

This simplified example is derived from our VectorSearchDatasets code.

Select embedding model

Many users will be interested in using deep learning models to embed their data. For an image this could be something like the multimodal vision-language model, CLIP. This model is available through the Hugging Face Transformers library, which we import here in order to load the model. We also import PyTorch and some data processing tools which will appear in the next step.

import svs
import torch
from transformers import AutoProcessor, CLIPProcessor, CLIPModel

model_str = "openai/clip-vit-base-patch32"
model = CLIPModel.from_pretrained(model_str)

Preprocess the data

You will need to prepare your data so that it can be processed by the embedding model. You should also apply any other preprocessing here, such as cropping images, removing extraneous text, etc.

For our example, let’s assume that the OpenImages dataset has been downloaded and we wish to preprocess the first 24 images. Here we use the HuggingFace AutoProcessor to pre-process the dataset to the format required by CLIP.

import pandas as pd
from PIL import Image

processor = AutoProcessor.from_pretrained(model_str)

image_list = []
n_img_to_process = 24
for img_id in range(0, n_img_to_process):
    image_fname = f'{oi_base_dir}/images/{img_id}.jpg'
    image = Image.open(image_fname)
    image_list.append(image)

print(f'Pre-processing {n_img_to_process} images')
inputs = processor(images=image_list, return_tensors="pt")

Embed the data to generate vectors

We then call the CLIP method to grab the features, or vector embeddings, associated with the images in our list. We also convert these embeddings from torch tensors to numpy arrays to enable their use in svs.

with torch.no_grad():
    print(f'Generating embeddings')
    embeddings = model.get_image_features(**inputs).detach().numpy()

Use or save the embeddings

Now that you have the embeddings as numpy arrays, you can directly pass them as inputs to svs functions. An example call to build a search index from the embeddings is shown below.

index = svs.Vamana.build(parameters, embeddings, svs.DistanceType.L2)

You may also save the embeddings into the commonly used vector file format *vecs with svs.write_vecs(). A description of the *vecs file format is given here.

svs.write_vecs(embeddings, out_file)

Other data format helper functions are described in our I/O and Conversion Tools documentation.